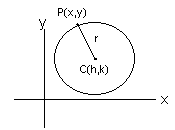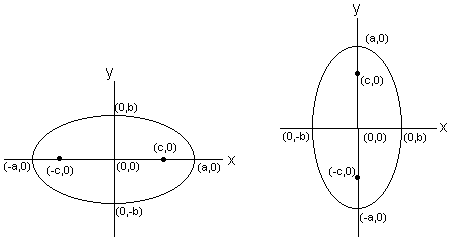Pre-AP PreCalculus
Mr. Keith W. Desrosiers
A BRIEF REVIEW OF THE CONIC SECTIONS
As you all recall, last year we spent a lot of our time studying the different conic
sections, how they were all formed (the intersection of a cone by a plane), and their general
formulas. Since that all seems like it occurred a long, long time ago in a galaxy far, far,
away (STAR WARS!), I thought it would be wise for us to all spend some time reviewing
the basics. So, here we go!
THE TECHNICAL DEFINITIONS:
-
Circle
- The collection of points in the Cartesian Plane which are equidistant from a fixed point
known as the center.
In the diagram below, the center is the point C(h,k) and the fixed distance is
labeled as r, the radius of the circle.
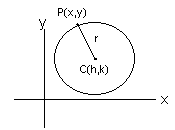
-
Parabola
- The collection of points in the Cartesian Plane which are equidistant from a fixed point
called the focus and the a fixed line known as the directrix.
In the diagrams below, the first parabola has the y-axis as its axis of symmetry, while the second
parabola has the x-axis as its axis of symmetry.

-
Ellipse
- The collection of points in
the Cartesian Plane such that the sum of the distances from two fixed points called the foci
is constant.
In the diagrams below, the first ellipse has its major axis on the x-axis and its minor axis on the y-axis, while the second ellipse
has its major axis on the y-axis and its minor axis on the x-axis.
The foci are located at the points (c, 0), (-c,0) and (0, c), (0, -c) respectively.
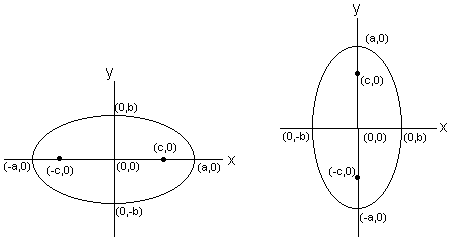
-
Hyperbola
- The collection of points in
the Cartesian Plane such that the absolute value of the differences of the distances from two
fixed points known as the foci is constant.
In the diagrams below, the first hyperbola has its transverse axis on the x-axis and its conjugate axis on the y-axis, while the second hyperbola
has its transverse axis on the y-axis and its conjugate axis on the x-axis.
The foci are located at the points (a, 0), (-a,0) and (0, a), (0, -a) respectively.

HISTORY OF THE CONIC SECTIONS
The words circle, ellipse, hyperbola, and parabola were first used by the members of the Pythagorean
society in ancient Greece around 540 B.C. These terms were used in connection with the regions
between the curves instead of the curves themselves as we refer to them today. Menaechmus (350 B.C.)
is credited with the first treatment of the terms as curves generated by sections of geometric solids.
However, it was Appolonius of Perga (about 225 B.C.), an astronomer of some fame in Greece, who
wrote an eight-book essay entitled Conic Sections . His work difered from others in that
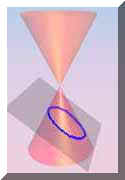
he obtained all of the conic sections from one double right cone intersected by a plane.
Appolonius stated that all variations in the shape of a conic section
could be obtained by varying the slope of the plane intersecting the conical surface.

Before you scroll down any further, take a moment or two and prove to yourself that
Appolonius' claim was indeed correct!
THE ANSWERS
| The Circle | The Ellipse | The Parabola | The Hyperbola
|
 |  |
 |  |
SOME THINGS TO THINK ABOUT
In PreCalculus we are going to continue our study of the conic sections by considering
the solutions to systems of conics contained in the Cartesian Plane, that is, multiple conic
sections and how they can intersect each other in the x-y plane.
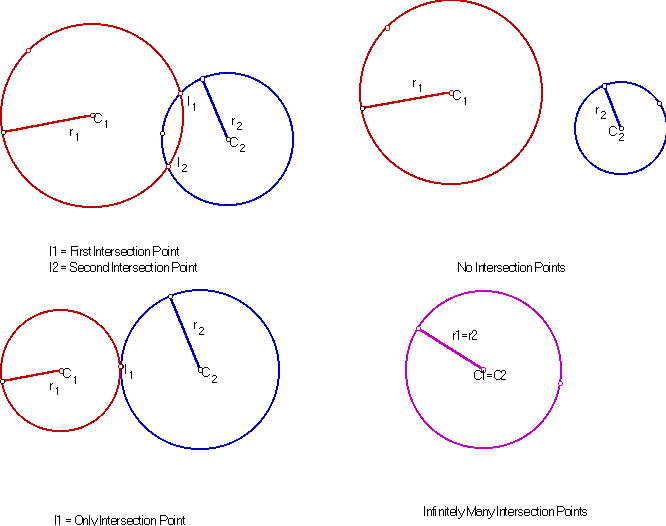
For example, two circles can intersect in each of the following ways:
- 0 points - two non-overlapping circles
- 1 point - two circles which are externally tangent
- 2 points - two overlapping circles
- infinitely many points - two identical circles laying upon one another
TONIGHT'S HOMEWORK ASSIGNMENT
For homework tonight, consider 7 of the following 9 cases involving systems of conic
sections. For each pair, you must consider the different ways that they can intersect one
another, list the different possibilities for the number of intersection points, and include
a diagram which supports your claim.
- A circle and a parabola
- A circle and an ellipse
- A circle and a hyperbola
- Two parabolas
- A parabola and an ellipse
- A parabola and a hyperbola
- Two ellipses
- An ellipse and a hyperbola
- Two hyperbolas
FOR NEXT CLASS
For the next class, you must review and have memorized the following formulas (these are
all in your Algebra II notes from last year):
| Conic Section | Standard Form of
Equation |
| Parabola (1) | y = a (x - h)2 + k |
| Parabola (2) | x = a (y - k) 2 + h |
| Circle | (x - h)2 + (y - k)2 = r2 |
| Ellipse(1) | (x - h)2 / a2 + (y - k)2 / b2 = 1
|
| Ellipse(2) | (y - k)2 / a2 + (x - h)2 / b2 = 1
|
| Hyperbola(1) | (x - h)2 / a2 - (y - k)2 / b2 = 1
|
| Hyperbola(2) | (y - k)2 / a2 - (x - h)2 / b2 = 1
|
| Hyperbola(3) | xy = k |
If you have any questions, please feel free to e-mail me at
kdserosi@hotmail.com
Click here to return to the main PreCalculus page.